20. Convergence of Positive Series

b.1. The Integral Test

If \(a_n=f(n)\) where \(f(x)\) is a continuous, positive, decreasing function on \([n_o,\infty)\), then \(\displaystyle \sum_{n=n_o}^\infty a_n\) is convergent if and only if \(\displaystyle \int_{n_o}^\infty f(x)\,dx\) is convergent.
\(\Longleftarrow\) Read this! It's easy.

Determine if \(\displaystyle \sum_{n=0}^\infty \dfrac{1}{1+n^2}\) is convergent or divergent.

The function \(f(x)=\dfrac{1}{1+x^2}\) is continuous, positive and decreasing, and \[\begin{aligned} \int_0^\infty &\dfrac{1}{1+x^2}\,dx =\left.\arctan x\rule{0pt}{10pt}\right|_0^\infty \\ &=\lim_{b\to\infty}\arctan b-\arctan 0 =\dfrac{\pi}{2} \end{aligned}\] which is finite. So \(\displaystyle \sum_{n=0}^\infty \dfrac{1}{1+n^2}\) is also convergent.

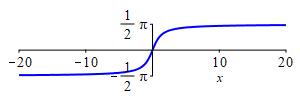
eg_arctan — \[ \lim_{x\to\infty}\arctan x=\dfrac{\pi}{2} \]

In practice, we do not bother to change the variable from \(n\) to \(x\), and simply compute \[ \int_0^\infty \dfrac{1}{1+n^2}\,dn =\left. \arctan n\rule{0pt}{10pt}\right|_0^\infty =\lim_{b\to\infty}\arctan b-\arctan 0 =\dfrac{\pi}{2} \]

Determine if \(\displaystyle \sum_{n=1}^\infty ne^{-n^2}\) is convergent or divergent or that the integral test does not apply.

The function \(f(n)=ne^{-n^2}\) is decreasing for \(n \ge 1\) because \[ f'(n)=e^{-n^2}+ne^{-n^2}(-2n)=(1-2n^2)e^{-n^2} \lt 0 \] for \(n \ge 1\).

\(\displaystyle \sum_{n=1}^\infty ne^{-n^2}\) is convergent.

The function \(f(n)=ne^{-n^2}\) is continuous and positive. It is also decreasing because \[ f'(n)=e^{-n^2}+ne^{-n^2}(-2n)=(1-2n^2)e^{-n^2} \lt 0 \] for \(n \ge 1\). Further, its integral is: \[\begin{aligned} \int_1^\infty &ne^{-n^2}\,dn =\left.-\,\dfrac{1}{2}e^{-n^2}\right|_1^\infty \\[10pt] &=\lim_{b\to\infty}\left[-\,\dfrac{1}{2}e^{-b^2}\right]-\left[-\,\dfrac{1}{2}e^{-1}\right] =\dfrac{1}{2e} \end{aligned}\] which is finite. So \(\displaystyle \sum_{n=1}^\infty ne^{-n^2}\) is convergent.

Determine if \(\displaystyle \sum_{n=1}^\infty e^{-n}\sin n\) is convergent or divergent or that the integral test does not apply.

The integral test requires that the funciton being tested is positive, continuous and decreasing.

The integral test does not apply because the terms are not strictly positive nor decreasing.

The function \(f(x)=e^{-x}\sin x\) oscillates between positive and negative values. Therefore the intergral test does not apply since the function is not strictly positive nor decreasing.

Determine if \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n}\) is convergent or divergent or that the integral test does not apply.

\(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n}\) is divergent.

The function \(f(x)=\dfrac{1}{x}\) is continuous, positive and decreasing and \[\begin{aligned} \int_1^\infty &\dfrac{1}{x}\,dx =\left.\ln x\rule{0pt}{10pt}\right|_1^\infty \\ &=\lim_{b\to\infty}[\ln b]-[\ln 1] =\infty-0=\infty \end{aligned}\] So \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n}\) is divergent.

The series \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n}\) is so important, it has a special name.

The series \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n}\) is called the harmonic series.

The harmonic series is the primary example of a divergent series. It is the special case of a \(p\)-series \(\displaystyle \sum_{n=1}^\infty \dfrac{1}{n^p}\) for which \(p=1\). The convergence of the other \(p\)-series is determined on the Next Page.

20. Convergence of Positive Series

b.1. The Integral Test

Heading